变换的应用

#

• 旋转
• 缩放
• 位置移动
• 光栅化

二维变换

#

缩放 (Scale Matrix)

#

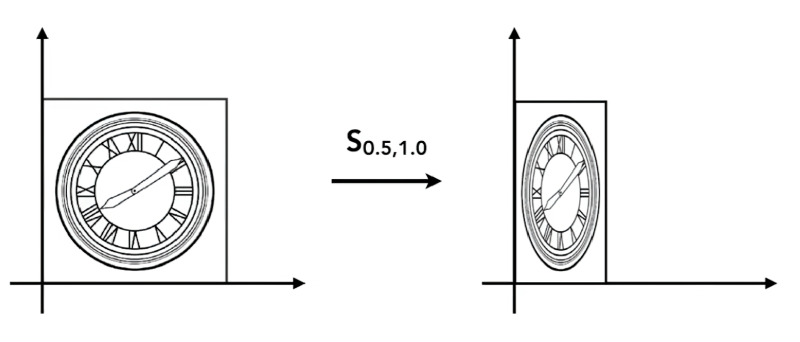
缩放变换是线性代数和计算机图形学中最基础的几何变换之一，用于将图形按比例放大或缩小.

• 数学表达 对于平面上任意一点 \((x, y)\)，经过缩放因子为 \(s\) 的变换后，新坐标 \((x', y')\) 为：

$$ \begin{cases} x' = s \cdot x \\ y' = s \cdot y \end{cases} $$

• 当 \(s > 1\) 时，图形放大。

• 当 \(0 < s < 1\) 时，图形缩小（如图中 \(s=0.5\)）。

• 当 \(s = 1\) 时，图形大小不变（恒等变换）。

• 矩阵形式

$$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$

翻转 (Reflection Matrix)

#

2D 翻转（反射）是把图形沿某条直线（轴）做镜像，得到对称图形。

常见：沿 x 轴翻转、沿 y 轴翻转、沿原点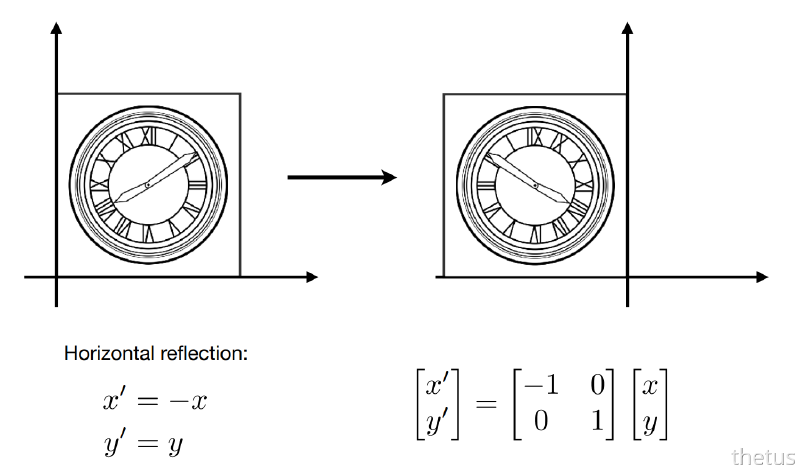

$$ \begin{cases} x' = -x \\ y' = y \end{cases} $$

• 矩阵形式

  $$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$

• 沿 x 轴：y 变号

• 沿 y 轴：x 变号

• 沿原点：x、y 都变号

• 矩阵都是对角矩阵，对角线上是 ±1

剪切 (Shear Matrix)

#

剪切变换(shear transformation)是空间线性变换之一，是仿射变换的一种原始变换。它指的是类似于四边形不稳定性那种性质，方形变平行四边形，任意一边都可以被拉长的过程。

$$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$

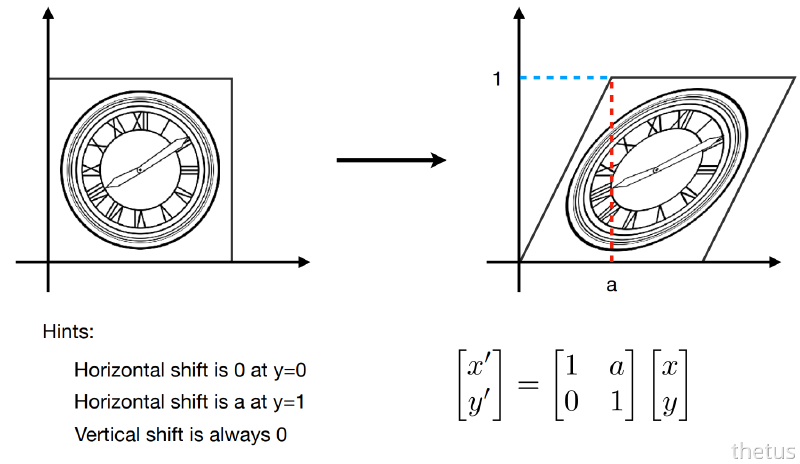
旋转 (Rotation Matrix)

#

$$ R_\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $$

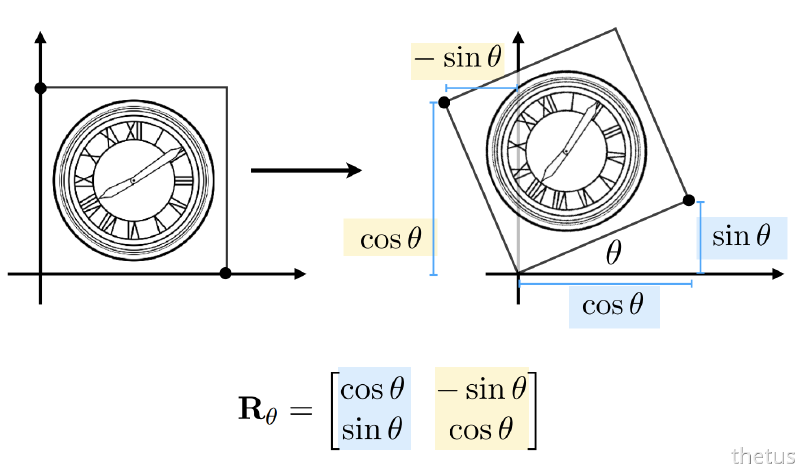
二维绕原点旋转矩阵推导

几何原理

取坐标系单位基向量，旋转后坐标直接构成矩阵列：

• 基向量 \(\boldsymbol{i}=(1,0)\) 逆时针转\(\theta\) → \((\cos\theta,\sin\theta)\)
• 基向量 \(\boldsymbol{j}=(0,1)\) 逆时针转\(\theta\) → \((-\sin\theta,\cos\theta)\)

关键记忆点

1. 第一列：x轴基向量旋转结果
2. 第二列：y轴基向量旋转结果
3. 负号固定在右上 \(-\sin\theta\) → 仅适用于 逆时针 $$boldsymbol{R}_{-\theta}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}$$
4. 顺时针旋转θ，负号移到左下： $$ \boldsymbol{R}_{-\theta}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix} $$

线性变换 = 矩阵(Linear transforms = Matrices)

#

核心结论

#

所有二维线性变换，都可以用一个同维度的方阵表示，这是线性代数、计算机图形学的底层核心。

线性变换的代数形式

#

二维平面内任意点 \((x,y)\)经过线性变换后得到新坐标 \((x',y')\)，满足一次齐次线性关系：

$$ \begin{cases} x' = ax + by \\ y' = cx + dy \end{cases} $$

矩阵形式（列向量标准式）

#

将线性方程组改写为矩阵 × 列向量的形式，是图形学、线性代数的通用写法：

$$ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$

向量简化形式

#

用向量符号统一表达，形式更简洁：

$$ \mathbf{x}' = \mathbf{M}\mathbf{x} $$

• \(\mathbf{x}\)：原坐标列向量 - \(\mathbf{x}'\)：变换后坐标列向量
• \(\mathbf{M}\)：线性变换矩阵（2×2方阵）

核心意义

#

1. 一切线性变换（旋转、缩放、翻转、剪切）本质都是一个矩阵
2. 变换的组合 = 矩阵的乘法
3. 变换的逆操作 = 矩阵的逆
4. 仅包含x、y一次项，无常数项、无高次项，才是线性变换

记忆要点

#

线性变换无平移、无常数偏移，仅由坐标的线性组合构成，可完全由方阵描述。

齐次坐标 (Homogeneous coordinates)

#

核心问题：平移变换（Translation）不属于线性变换，无法用普通矩阵乘法表示,引入齐次坐标之后,平移和旋转能统一用矩阵乘法

• 统一平移矩阵和线性变换矩阵，使其可以直接参与运算
• 为向量拓展一个维度，使得一个三维变量可以区分表示为向量和点（w为1为点，w为0为向量，保证向量的平移不变性）

原始仿射变换公式（乘法 + 加法，无法统一）：

$$ \begin{bmatrix}x' \\ y'\end{bmatrix}=\begin{bmatrix}a & b \\c & d\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}+\begin{bmatrix}t_x \\ t_y\end{bmatrix} $$

解决方案：引入齐次坐标，将平移也转化为矩阵乘法形式

2D 平移矩阵（齐次坐标形式）：

$$ \begin{bmatrix}x' \\ y' \\ 1\end{bmatrix} = \begin{bmatrix}1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \\ 1\end{bmatrix} = \begin{bmatrix}x + t_x \\ y + t_y \\ 1\end{bmatrix} $$

向量平移验证（w=0，不受影响）：

$$ \begin{bmatrix}1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \\ 0\end{bmatrix} = \begin{bmatrix}x \\ y \\ 0\end{bmatrix} $$

点与向量的运算规则

运算	结果	齐次坐标验证
向量 + 向量	向量	(x₁,y₁,0) + (x₂,y₂,0) = (x₁+x₂, y₁+y₂, 0)
点 - 点	向量	(x₁,y₁,1) - (x₂,y₂,1) = (x₁-x₂, y₁-y₂, 0)
点 + 向量	点	(x,y,1) + (dx,dy,0) = (x+dx, y+dy, 1)
点 + 点	中点	(x₁,y₁,1) + (x₂,y₂,1) = (x₁+x₂, y₁+y₂, 2) → 归一化 → (x₁+x₂/2, y₁+y₂/2, 1)

点 + 点 = 中点 的解释

两个点相加得到 (x₁+x₂, y₁+y₂, 2)，w=2 不是标准形式 归一化：除以 w，得到 (x₁+x₂/2, y₁+y₂/2, 1)，这正是两点的中点

二维齐次坐标

#

$$\text{点: } \begin{bmatrix} x \\ y \\ 1 \end{bmatrix},\quad \begin{bmatrix} x \\ y \\ w\end{bmatrix} \text 表示点 \begin{bmatrix} \frac{x}{w} \\ \frac{x}{w} \\ 1 \end{bmatrix}, \quad \text{向量: } \begin{bmatrix} x \\ y \\ 0 \end{bmatrix}$$

二维仿射变换

#

仿射映射 = 线性映射 + 平移变换

$$\begin{bmatrix}x' \\ y'\end{bmatrix}=\begin{bmatrix}a & b \\c & d\end{bmatrix}\begin {bmatrix}x \\ y\end{bmatrix}+\begin {bmatrix}t_x \\ t_y\end{bmatrix}$$

使用齐次坐标表示仿射变换

$$\begin{bmatrix} x' \\ y' \\ 1\end{bmatrix}=\begin{bmatrix} a & b & t_x \\c & d & t_y \\0 & 0 & 1 \\\end{bmatrix} \cdot\begin {bmatrix} x \\ y \\ 1 \end {bmatrix}$$

• 缩放 (Scale Matrix)

$$ \mathbf{S}(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

• 翻转 (Reflection Matrix)

$$ \mathbf{R}(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

• 平移 (Translation Matrix)

$$ \mathbf{T}(t_x, t_y) = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} $$

逆变换

#

M⁻¹ 在矩阵和几何意义上都是变换 M 的逆。

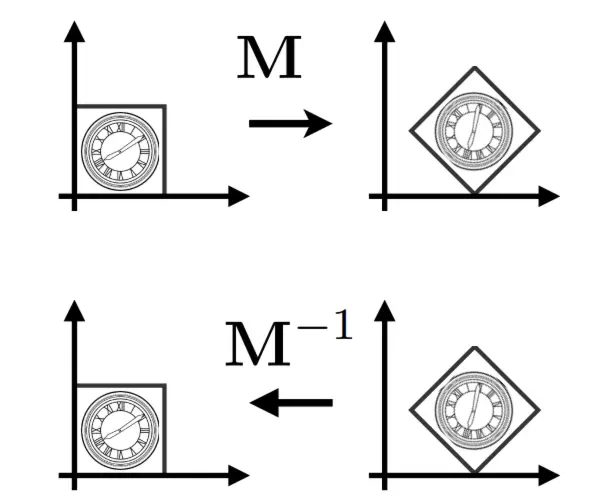
组合变换

#

• 平移、旋转、缩放变换可以组合起来

• 变换的顺序很重要，不能调换（矩阵的乘法不满足交换律）

  $$ T_{(1,0)} \cdot R_{45} \neq R_{45} \cdot T_{(1,0)} $$

• 可以通过矩阵的乘法来实现组合变换，从右到左的操作

  $$ A_n(\dots A_2(A_1(\mathbf{x}))) = \mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

示例：先旋转 45 度，再平移 (1, 0)

$$ T_{(1,0)} \cdot R_{45} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos 45^\circ & -\sin 45^\circ & 0 \\ \sin 45^\circ & \cos 45^\circ & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} \cos 45^\circ & -\sin 45^\circ & 1 \\ \sin 45^\circ & \cos 45^\circ & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$

• 变换顺序：矩阵从右到左依次应用
• 复合矩阵：通过矩阵乘法，将多个变换合并为一个矩阵，提高计算效率。
• 齐次坐标：使用 \(\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\)​​ 这种三维向量，是为了让平移也能通过线性变换（矩阵乘法）来表示。

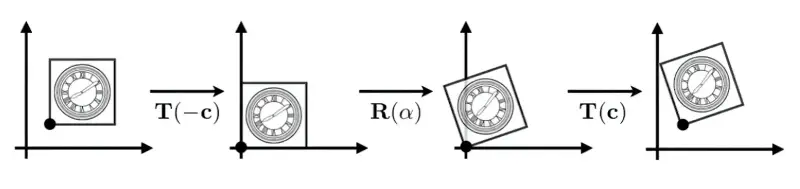
旋转中心不在原点：中心移动到原点->旋转->中心移动到原位置

$$ \mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c}) $$

三维变换

#

$$ \begin{aligned} & \text{三维点(3D Point)}: (x, y, z, \mathbf{1})^T \\ &\text{三维向量(3D Vector)}: (x, y, z, \mathbf{0})^T \end{aligned} $$

一般来说，(x, y, z, w)（其中 w ≠ 0）表示一个 3D 点：

$$ \text{3D Point} = \left( \frac{x}{w}, \frac{y}{w}, \frac{z}{w} \right) $$

三维仿射变换

#

$$ \underbrace{ \begin{pmatrix} x' \\ y' \\ z' \\ 1 \end{pmatrix} }_{\text{变换后点}} = \underbrace{ \begin{pmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix} }_{\text{4×4 仿射变换矩阵}} \cdot \underbrace{ \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} }_{\text{原始点（齐次坐标）}} $$

$$ \begin{aligned} x' &= a x + b y + c z + t_x \\ y' &= d x + e y + f z + t_y \\ z' &= g x + h y + i z + t_z \\ 1 &= 0 x + 0 y + 0 z + 1 \end{aligned} $$

顺序（同二维）：先线性变换再平移

缩放(Scale)和平移(Translation)

#

$$ \text{Scale: } \mathbf{S}(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$$$ \text{Translation: } \mathbf{T}(t_x, t_y, t_z) = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

旋转 (Rotation)

#

绕坐标轴旋转

#

旋转矩阵的性质

旋转θ的矩阵：

$$ R_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} $$

旋转-θ的矩阵：

$$ R_{-\theta} = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} $$

可以发现: \(R_{-\theta}\)恰好是 \(R_{\theta}\) 的转置，即：

$$ R_{-\theta} = R_\theta^T $$

因此:

$$ R_\theta^{-1} = R_\theta^T $$

这说明旋转矩阵是正交矩阵，其逆矩阵等于其转置矩阵。

绕X轴旋转

$$ \mathbf{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

绕Y轴旋转

$$ \mathbf{R}_y(\alpha) = \begin{pmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

为什么是 -sina : xoz是顺时针的，顺时针旋转了a,相当于逆时针旋转了-a，旋转是逆时针的，-a的旋转矩阵要求逆，也就是转置

• Z 轴（k）向右（X 正）偏 → 必然带动 X 轴（i）向下（Z 负）偏；
• 负号仅代表方向，sinα的绝对值是偏移的 “长度”。 绕Z轴旋转

$$ \mathbf{R}_z(\alpha) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

欧拉角

#

• 欧拉角描述相对于初始状态的变换，只和最终状态有关，与过程无关。

由于欧拉角（Euler）表示旋转时存在旋转轴的次序，当中间旋转轴旋转使得前后两个轴对齐时，就失去了一个旋转自由度，出现万向节死锁。可以使用四元数（Quaternion）解决该问题。

$$ \text{欧拉角:乘法顺序：从右到左执行} \quad \\\ \mathbf{R}_{xyz}(\alpha, \beta, \gamma) = \mathbf{R}_x(\alpha) \mathbf{R}_y(\beta) \mathbf{R}_z(\gamma) $$

BILIBILI视频 【无伤理解欧拉角中的“万向死锁”现象】

罗德里格斯旋转公式（Rodrigues’ Rotation Formula）

#

$$ \mathbf{R}(\mathbf{n}, \alpha) = \cos(\alpha) \mathbf{I} + (1 - \cos(\alpha)) \mathbf{n} \mathbf{n}^T + \sin(\alpha) \underbrace{ \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix} }_{\mathbf{N}} $$

其中,反对称矩阵N 为:

$$ \mathbf{N} = \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix} $$

推导: # 3D下的旋转矩阵 https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_04_supp.pdf

四元数

#

本课程不讲