向量#
三种看待向量的观点#
- 物理:向量是空间中具有方向和长度的箭头
- 计算机科学:向量是有序的数字列表
- 数学:向量的相加和相乘有意义
向量法则#
- 向量加法
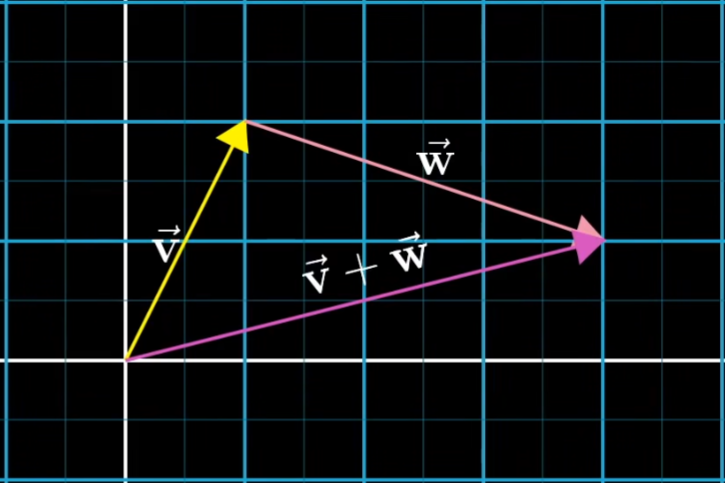
为什么向量加法遵循平行四边形？
在几何角度上，两个向量相加在几何上是把两个向量沿着平行于坐标系的方向平移，将两个向量首尾相接，此时终点和“和向量”所指向的终点一致。若把向量看成对特定运动的一种描述，其运动的结果一致。
- 向量乘法
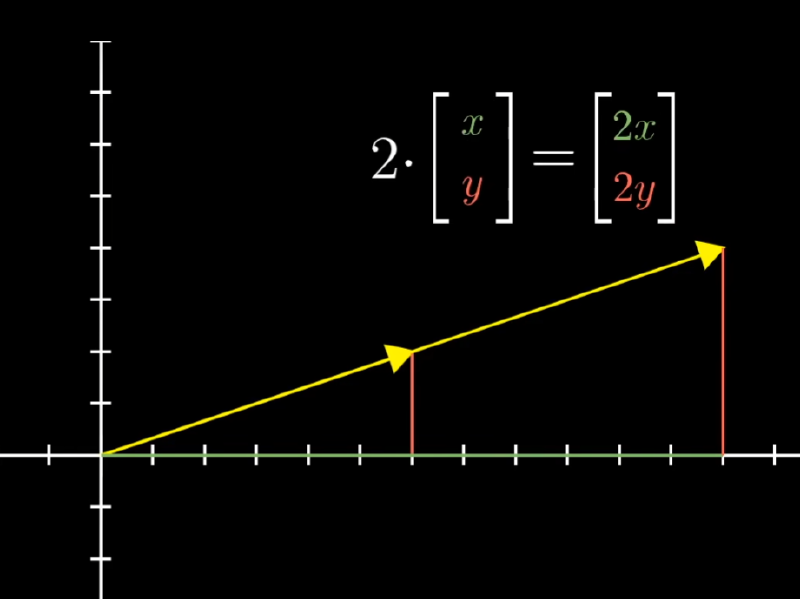
向量乘法的几何意义
对向量按照“标量”(Scalars，在此处可以和number替换理解)“来缩放”(Scaling). 具体来说是对向量的: 拉伸、缩短、反转。
线性组合#
- 基向量：单位向量
i，j是坐标系xy的基向量
- 线性组合：两个数乘向量的和成为这两个向量的线性组合
平面中任意两个基向量（非共线/非0向量）能组成平面内所有向量
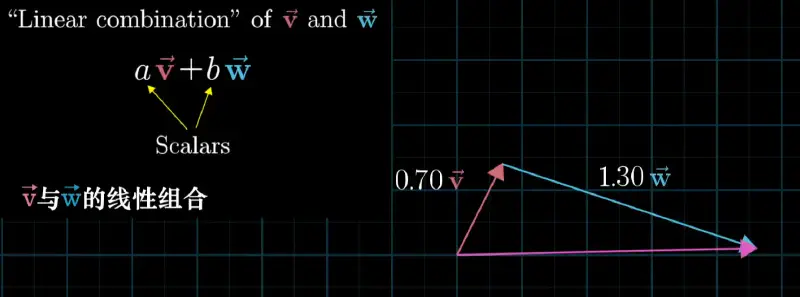
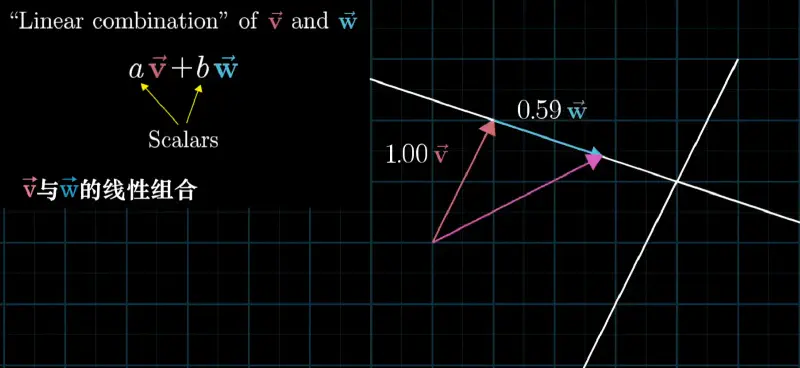
张成空间#
张成空间：给定基向量的所有线性组合的集合，将箭头看作点时，共线时为直线非共线为平面。 一组向量 \(\{v_1, v_2, \dots, v_k\}\)的张成空间是这些向量的所有可能线性组合的集合。 即：
$$ \text{Span}\{v_1, v_2, \dots, v_k\} = \left\{ c_1 v_1 + c_2 v_2 + \cdots + c_k v_k \,\middle|\, c_1, c_2, \dots, c_k \in \mathbb{R} \right\} $$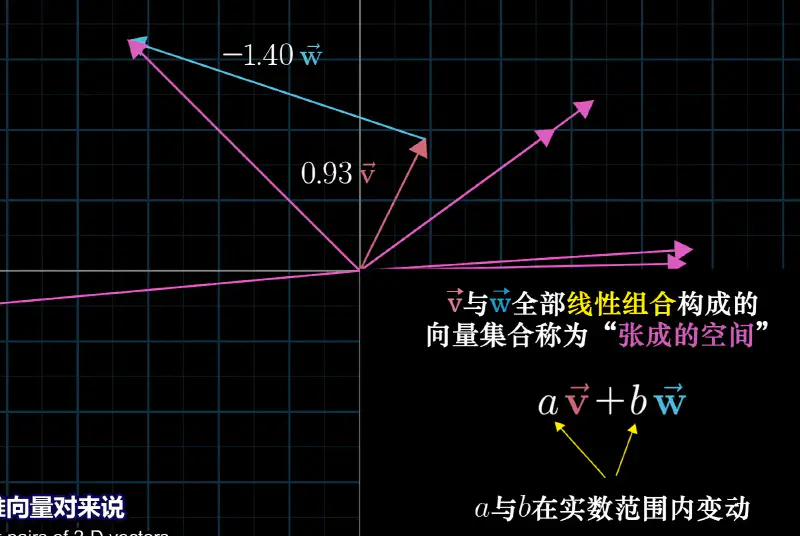
三维空间的张成空间
如果第三个向量恰好落在前两个向量所张成的平面上,所张成的空间不变.
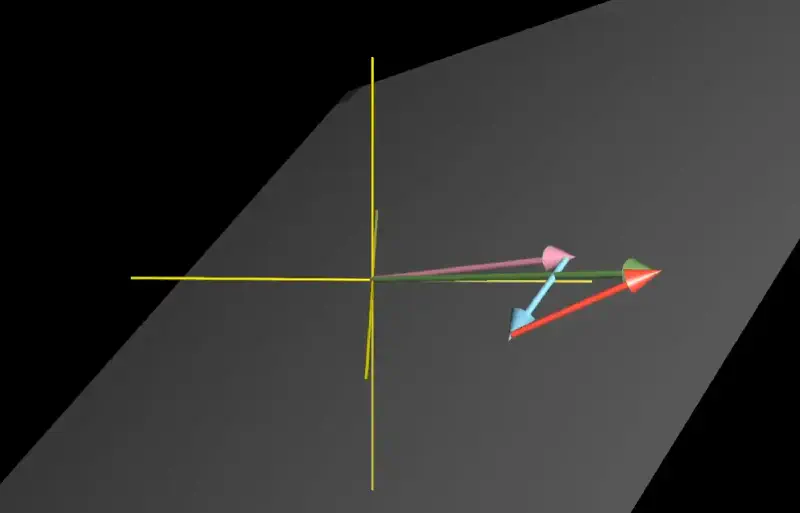
当三个向量非共面时,张成空间是整个三维空间,线性组合能组合成三维空间的任意向量.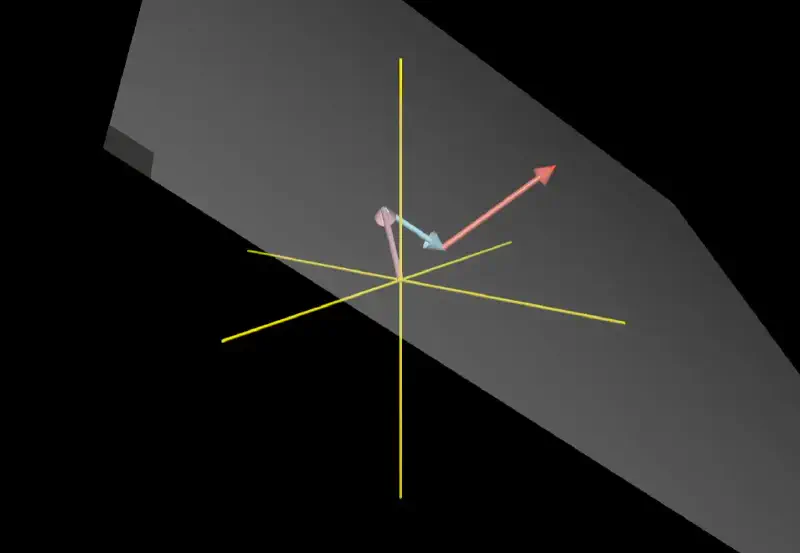
线性相关#
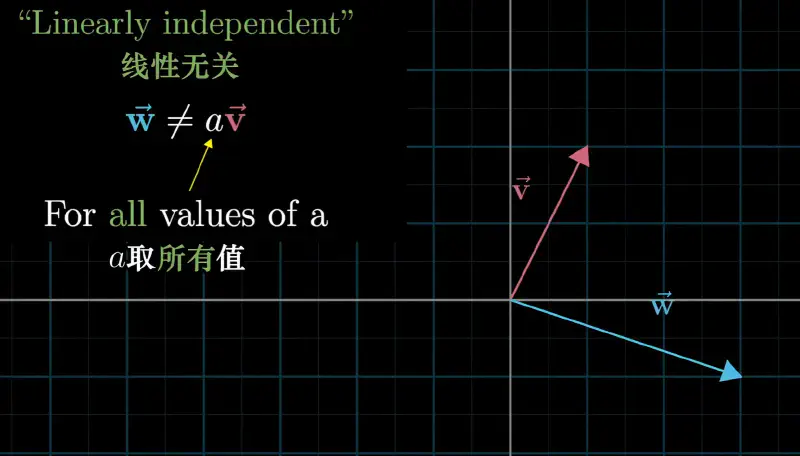
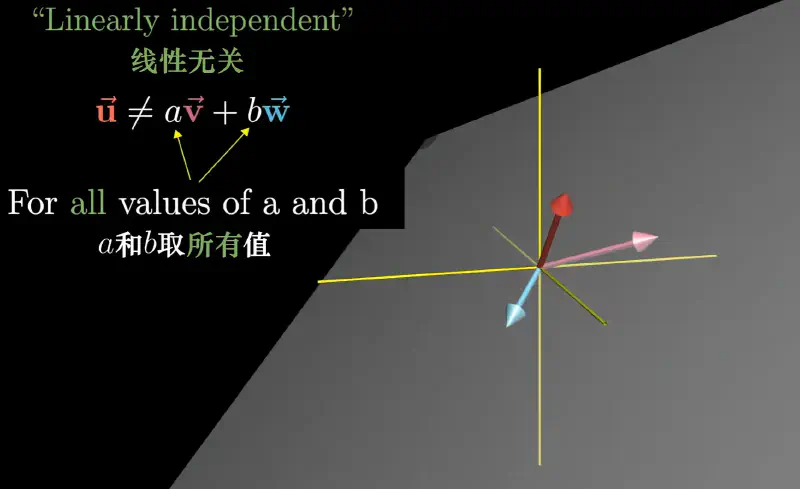
线性无关#
